Alloy is a “lightweight formal methods” tool that has been used primarily to explore abstract software designs. “Alloy” refers to both a logic (which combines elements of first order logic and relational calculus) and a tool for analyzing models specified in that logic. The language is in fact quite general and people have found a wide range of applications of the tool — I’m sure many that the original developers (led by Daniel Jackson) never envisioned.
In this post I will show an Alloy model I made for my course Logic in Computer Science. We spend a good bit of time in the course doing derivations (formal proofs) by Natural Deduction (ND), first for Propositional Logic (PL), then for First Order Logic. Here are the rules of ND for PL as presented in Rigorous Software Development by Almeida, Frade, Pinto and de Sousa, Springer, 2011:

A judgment in this logic is a sequent of the form \(\Gamma\vdash A\), where \(\Gamma\) is a set of (propositional) formulas and \(A\) is a formula. The rules specify when you can conclude new judgments from old. For example, rule (Ax) says that one can always conclude \(\Gamma\cup\{A\}\vdash A\) for any set \(\Gamma\) and formula \(A\) (\(\Gamma, A\) being shorthand for the set \(\Gamma\cup\{A\}\)). Rule \((\textrm{I}_\neg)\) says that if one has derived \(\Gamma,A\vdash\bot\) then one may conclude \(\Gamma\vdash\neg A\). Here is a derivation of the “law of the excluded middle”, \(\emptyset\vdash p\vee\neg p\):
\begin{array}{rrcll} 0. & \neg(p\vee\neg p), \neg p & \vdash & \neg p & (\textrm{Ax}) \\ 1. & \neg(p\vee\neg p), \neg p & \vdash & p\vee\neg p & (\textrm{I}_{\vee2})0\\ 2. & \neg(p\vee\neg p), \neg p & \vdash & \neg(p\vee\neg p) & (\textrm{Ax})\\ 3. & \neg(p\vee\neg p), \neg p & \vdash & \bot & (\textrm{E}_\neg)1,2\\ 4. & \neg(p\vee\neg p) & \vdash & p & (\textrm{RAA})3\\ 5. & \neg(p\vee\neg p) & \vdash & \neg(p\vee\neg p) & (\textrm{Ax})\\ 6. & \neg(p\vee\neg p) & \vdash & p\vee\neg p & (\textrm{I}_{\vee1})4\\ 7. & \neg(p\vee\neg p) & \vdash & \bot & (\textrm{E}_\neg)6,5\\ 8. & & \vdash & p\vee\neg p & (\textrm{RAA})7 \end{array}
The following Alloy model specifies an ND derivation for PL. Using this model, the Alloy Analyzer can automatically find a derivation for a given sequent. It is a good demonstration of the expressiveness of the Alloy logic. In 218 lines (including comments), the syntax of PL, derivations, and the rules of ND are fully specified, as well as several examples:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 |
/* Alloy model of Natural Deduction for Propositional Logic Stephen Siegel, University of Delaware, Nov. 2021 This model will find ND derivations for sequents in PL, i.e., judgments of the form S |- f, where S is a set of PL formulas (the antecedents) and f is a PL formula (the consequent). */ -- derivations are trees but can be ordered for readability, -- though this can increase runtime significantly. -- children of node d always occur before d in the total order... open util/ordering[Derivation] /* PL Formulas */ abstract sig Formula { } -- all PL formulas one sig False extends Formula { } -- the formula "False" sig Prop extends Formula { } -- propositions abstract sig Op {} one sig NOT, AND, OR, IMPLIES extends Op {} sig CompoundFormula extends Formula { -- formulas formed by a connective op: one Op, -- the operator arg1: one Formula, -- argument 1 (required) arg2: lone Formula -- argument 2 (optional) }{ op = NOT iff no arg2 -- only NOT takes 1 argument } -- no formula can occur as a sub-formula of itself... fact wellFormedFormula { no f: Formula | f in f.^( arg1 + arg2 ) } /* Derivations */ abstract sig Rule {} -- enumeration of the rule schema for ND one sig Ax, RAA, EAnd1, EAnd2, IAnd, EOr, IOr1, IOr2, EImp, IImp, ENot, INot extends Rule {} sig Derivation { -- a derivation is a recursive (tree-like) structure: rule: one Rule, -- the rule of which this derivation is an instance premise1, premise2, premise3: lone Derivation, -- at most 3 sub-derivations antecedents: set Formula, -- left side of sequent of conclusion consequent: one Formula -- right side of sequent of conclusion } fun antes[d: Derivation]: set Formula { d.antecedents } fun form[d: Derivation]: one Formula { d.consequent } fun premise[]: Derivation->Derivation { premise1 + premise2 + premise3 } fact wellFormedDerivation { -- each derivation is the application of a rule all d: Derivation | { d.premise in prevs[d] -- use only if ordering Derivation ax[d] or eAnd1[d] or eAnd2[d] or iAnd[d] or eOr[d] or iOr1[d] or iOr2[d] or eImp[d] or iImp[d] or eNot[d] or iNot[d] or raa[d] } } -- use this to say every Derivation is used in the derivation -- that means the scope for Derivation must be exact, rather -- than upper bound pred exactRoot[d: Derivation] { d.*premise = Derivation } -- When ordering, -- the scope is specified exactly rather than as an upper bound, -- so need to do something with the derivations that are not used. -- say all derivations not reachable from root d just stutter d pred isRoot[d: Derivation] { all d1: Derivation - d.*premise | { d1.rule = d.rule d1.premise1 = d.premise1 d1.premise2 = d.premise2 d1.premise3 = d.premise3 d1.antecedents = d.antecedents d1.consequent = d.consequent } } /* Derivation rules */ -- Rule 1: Ax: S,f |- f pred ax[d: Derivation] { d.rule = Ax and no d.premise and form[d] in antes[d] } -- Rule 2: Reductio-Ad-Absurdum: if S,!f |- False then S |- f pred raa[d: Derivation] { d.rule = RAA and no d.premise2 + d.premise3 let d1 = d.premise1 | form[d1] = False and some g: CompoundFormula | g.op = NOT and g.arg1 = form[d] and antes[d1] = antes[d] + g } -- Rule 3: Eliminate-and-1: if S |- f&g then S |- f pred eAnd1[d: Derivation] { d.rule = EAnd1 and no d.(premise2 + premise3) antes[d.premise1] = antes[d] let h = form[d.premise1] | h.op = AND and h.arg1 = form[d] } -- Rule 4: Eliminate-and-2: if S |- f&g then S |- g pred eAnd2[d: Derivation] { d.rule = EAnd2 and no d.(premise2 + premise3) antes[d.premise1] = antes[d] let h = form[d.premise1] | h.op = AND and h.arg2 = form[d] } -- Rule 5: Introduce-And: if S |- f and S |- g then S |- f&g pred iAnd[d: Derivation] { d.rule = IAnd and no d.premise3 let d1 = d.premise1, d2=d.premise2, h=form[d] | antes[d1] = antes[d2] and antes[d1] = antes[d] and h.op = AND and h.arg1 = form[d1] and h.arg2 = form[d2] } -- Rule 6: Eliminate-Or: if S |- f1|f2 and S,f1 |- h and S,f2 |- h then S |- h pred eOr[d: Derivation] { d.rule = EOr let S = antes[d], d1 = d.premise1, d2=d.premise2, d3=d.premise3 | antes[d1] = S and antes[d2] = S + form[d1].arg1 and antes[d3] = S + form[d1].arg2 and form[d1].op = OR and form[d2] = form[d] and form[d3] = form[d] } -- Rule 7: Introduce-Or-1: if S |- f then S |- f|g pred iOr1[d: Derivation] { d.rule = IOr1 and no d.premise2 + d.premise3 antes[d.premise1] = antes[d] form[d].op = OR and form[d].arg1 = form[d.premise1] } -- Rule 8: Introduce-Or-2: if S |- f then S |- g|f pred iOr2[d: Derivation] { d.rule = IOr2 and no d.premise2 + d.premise3 antes[d.premise1] = antes[d] form[d].op = OR and form[d].arg2 = form[d.premise1] } -- Rule 9: Eliminate-Implies: if S |- f->g and S |- f then S |- g pred eImp[d: Derivation] { d.rule = EImp and no d.premise3 let d1 = d.premise1, d2 = d.premise2 | { antes[d1] = antes[d] and antes[d2] = antes[d] form[d2].op = IMPLIES and form[d2].arg1 = form[d1] form[d] = form[d2].arg2 } } -- Rule 10: Introduce-Implies: if S,f |- g then S |- f->g pred iImp[d: Derivation] { d.rule = IImp and no d.premise2 + d.premise3 let d1 = d.premise1, h=form[d] | h.op = IMPLIES and antes[d1] = antes[d] + h.arg1 and form[d1] = h.arg2 } -- Rule 11: Eliminate-Not: if S |- !f and S |- f then S |- g pred eNot[d: Derivation] { d.rule = ENot and no d.premise3 let d1 = d.premise1, d2 = d.premise2 | antes[d1] = antes[d] and antes[d2] = antes[d] and form[d2].op = NOT and form[d2].arg1 = form[d1] } -- Rule 12: Introduce-Not: if S,f |- False then S |- !f pred iNot[d: Derivation] { d.rule = INot and no d.premise2 + d.premise3 let d1 = d.premise1 | form[d].op = NOT and antes[d1] = antes[d] + form[d].arg1 and form[d1] = False } /* Examples */ -- A |- A (simple application of Ax rule) pred ax1[d: Derivation] { isRoot[d] let f = antes[d] | one f and f=form[d] and f in Prop } -- A & B |- B & A (and is commutative) pred andCommute[d: Derivation] { isRoot[d] let f = antes[d], g = form[d] | one f and g.op = AND and f.(arg1+arg2) in Prop and f.op = AND and g.arg1 = f.arg2 and g.arg2 = f.arg1 and f.arg1 != f.arg2 } -- A & (B | C) |- (A & B) | (A & C) (and distributes over or) pred dist1[d: Derivation] { isRoot[d] let f = antes[d] | one f and f.op = AND and f.arg2.op = OR and let a = f.arg1, b = f.arg2.arg1, c = f.arg2.arg2, g = form[d] | { a+b+c in Prop a != b and a != c and b != c g.op = OR g.arg1.op = AND and g.arg1.arg1 = a and g.arg1.arg2 = b g.arg2.op = AND and g.arg2.arg1 = a and g.arg2.arg2 = c } } -- |- P | !P (Law of the Excluded Middle) pred LEM[d: Derivation] { isRoot[d] no antes[d] let f = form[d], p = f.arg1, f2 = f.arg2 | f.op = OR and p in Prop and f2.op = NOT and f2.arg1 = p } -- |- !(A & B) -> (!A | !B) pred deMorgan1[d: Derivation] { exactRoot[d] no antes[d] let f = form[d], f1 = f.arg1, f2 = f.arg2, f11=f1.arg1, f21 = f2.arg1, f22 = f2.arg2, a = f11.arg1, b = f11.arg2 | a != b and a+b in Prop and f.op = IMPLIES and f1.op = NOT and f11.op = AND and f2.op = OR and f21.op = NOT and f21.arg1 = a and f22.op = NOT and f22.arg1 = b } /* Runs. Solving times shown for Plingeling on MacBook Pro M1 */ run ax1 -- 1s run andCommute for 2 Prop, 5 Formula, 4 Derivation -- 1s run dist1 for 3 Prop, 9 Formula, 13 Derivation -- 7s run LEM for 1 Prop, 5 Formula, 9 Derivation -- 10s run deMorgan1 for 2 Prop, 10 Formula, 15 Derivation -- varies wildly |
The model defines the syntax for a propositional logic formula, and then defines the structure of a derivation, which is a recursive (tree-like) structure. Each node is the application of one of 12 rules, has some number (\(\leq 3\)) of children (premises, or sub-derivations), and a conclusion, which is a sequent of the form \(S\vdash f\), where \(S\) is a set of formulas (the antecedents) and \(f\) is a formula (the consequent). Then there is a series of examples where I describe the desired sequent and ask Alloy to find a derivation of it.
From the Alloy Analyzer menu, if we select to execute the “run LEM…” command, the result, after a few seconds, is an instance of the model. The instance can be viewed in Alloy’s Table view mode. The first table shows the Formulas. In addition to the atomic formulas False (\(\bot\)) and Prop0 (\(p\)), the following three compound formulas appear:
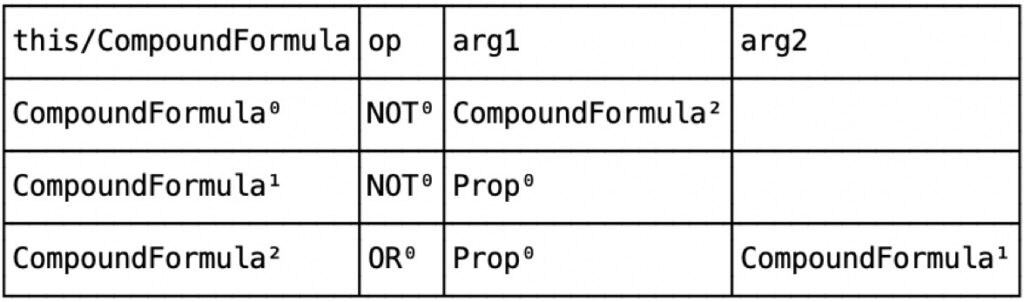
These represent, in order: \(\neg(p\vee\neg p)\), \(\neg p\), and \(p\vee\neg p\). Now here is the derivation, exactly as it appears in Alloy’s Table view:
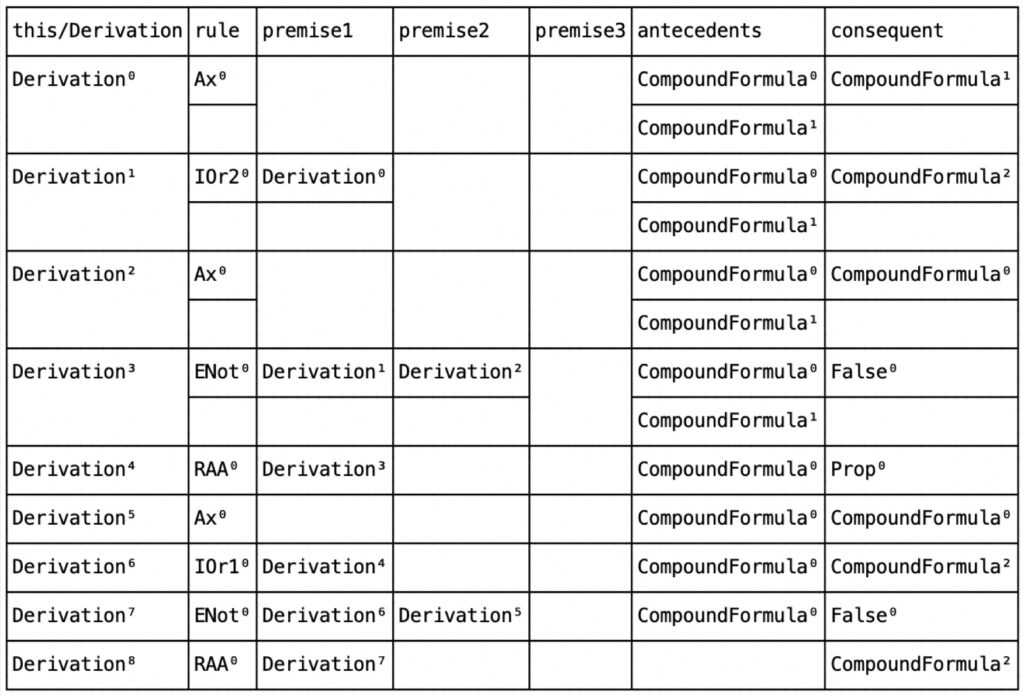
which is exactly the derivation one would write by hand and is shown above.
Notice that we never had to specify any algorithm to find derivations. Rather, we just had to tell Alloy what a derivation looks like, and Alloy—and the PLingeling SAT solver—do the hard work of finding something matching our description.
Nice! I am constantly surprised by all the novel applications of Alloy people come up with.
Do you think this could be extended to a model for ND for First Order Logic? I imagine the SAT problems would really start to blow up…