Verification of a Barrier Algorithm, part 1

The concurrency flag, aka binary semaphore, is the most primitive synchronization structure. It is the basic concurrency building block, from which all manner of more complex synchronization algorithms can be implemented.

A concurrency flag has two states: up or down. It supports two atomic operations: lower and raise. The lower operation is enabled only when the flag is up, in which case it changes the state to down. If lower is invoked when the flag is down, it blocks until the flag is up. The raise operation is only defined when the flag is down, in which case it changes the state to up. It is erroneous to attempt to raise the flag when it is already up. Note the asymmetry: it is never erroneous to invoke lower — the operation will simply block until the flag can be lowered. Raise never blocks, but it should only be invoked when the flag is down.

(The concept of semaphore in concurrency theory is due to Edsker Dijkstra. He used the letter V to represent the raise operation, and P for the lower operation. V stands for verhogen, Dutch for “to raise”. P may stand for passering — “passing” — or probeer te verlagen — “try to decrease”.)

This post looks at the problem of designing a barrier protocol using concurrency flags. A barrier is a synchronization operation involving a set of threads. The basic property of a barrier is that no thread shall leave the barrier until all threads in the set have entered the barrier. A second desirable property is no unnecessary delay — once all threads have entered the barrier, all threads should be able to depart without unnecessary blocking. A third desirable property is reusability — the barrier should be able to be invoked multiple times in a program and work correctly.

It is easy to design a barrier with the first property but not the second: never let any thread leave the barrier. We will see it is actually tricky to design a barrier with all three properties.

The case of two threads is a good place to start. We can implement a 2-thread barrier using two flags, f1 and f2, both initially down. The protocol is

The first operation that will execute in this protocol is thread 1’s raise f1. After that, thread 1 must block, as f2 is down, but thread2 can now lower f1. Thread 1 is still blocked, so thread 2 raises f2 and now thread 2 may depart the barrier. Thread 1 may now lower f2 and depart.

The basic barrier property holds: if thread 1 arrives first to the barrier, it raises f1 but then blocks at the lower f2 and cannot proceed until thread 2 arrives and eventually raises f2. If thread 2 arrives at the barrier first, it blocks, at the lower f1. The property of no unnecessary delay is admittedly vague, but at a minimum it requires that once every thread arrives, eventually every thread should be able to leave, and that is the case for this protocol. The third property, reusability, also holds — I’ll hold off on a proof of that, but for now observe that at least the flags are returned to their original state after both threads leave the barrier.

It is helpful to think of “raise” as sending a signal, and “lower” as receiving that signal. Then we can view the protocol as follows:

First thread 1 sends a signal to thread 2. Thread 2 receives the signal and then sends a signal to thread 1. Thread 1 receives the signal.

We can obtain a more rigorous analysis of the protocol by examining its state space. The state space is a directed graph in which the nodes are program states, and an edge represents an atomic transition from one state to another. A state encodes the values of all variables in the program, including the location (program counter) of each thread, and the state of each flag. The reachable state space is the subgraph consisting of the states and transitions that are reachable from the initial state.

Let’s put our 2-thread barrier in a loop, to analyze reusability, and also label the two statements in each thread to provide values for the location:

When Thread 1’s location is 0, its next action will be the raise operation, after which it moves to location 1. From location 1 (assuming f2 is up), Thread 1 lowers f2 and moves to location 0, etc. A state of this program may be represented as a tuple [pc1, pc2, f1, f2], where pc1 and pc2 are locations in {0,1}, and f1 and f2 are in {U,D} (U=up, D=down). The initial state is [0,0,D,D]. From that state, only one transition is enabled, Thread 1’s raise of f1, and the resulting state is [1,0,U,D]. Continuing in this way, we obtain the following reachable state space:

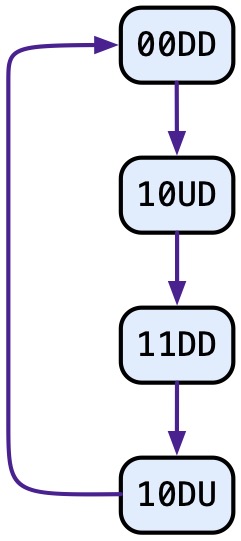
The reachable state space shows us that the barrier program is deterministic: at each reachable state, there is one and only one enabled transition. Furthermore, we may interpret location 0 as being “outside” the barrier and location 1 as being “inside” the barrier. The reachable state space also shows that no thread will leave the barrier until both have entered: the leaving transitions are the two transitions that change a 1 to a 0; the entering transitions change a 0 to a 1. The only path from the initial state proceeds with two enters, followed by two exits, repeated forever. This also shows there is no unnecessary delay (or at least all threads eventually leave the barrier), and the barrier is reusable, since we are doing all of this inside a loop. Incidentally we can also check that flags are used correctly, i.e., there is never an attempt to raise a flag that is already up.

One of the first times I showed this 2-flag barrier in a class, a student asked whether both threads could raise first, then lower. I thought about it. The two raises could occur in either order — fine, you end up at the same state in either case. Then the two lowers could happen in either order — also fine. And neither lower could occur without the raise in the other thread occurring first, guaranteeing the basic barrier property. So I said it looked right, but I would check. I went back to the office and thought about it. The program would become:

Let’s do the same state-enumeration analysis. This time the reachable state space looks like this:

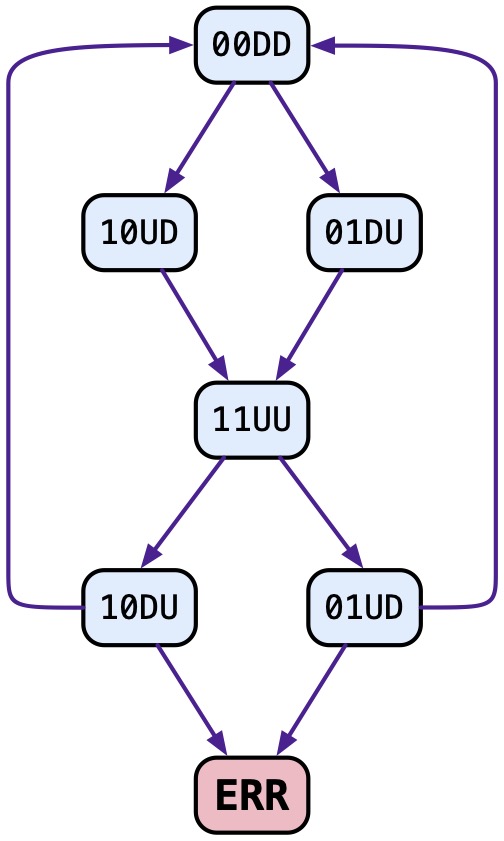
The problem occurs from a state like [0,1,U,D]. From this state, Thread 2 could lower f1 and return to location 0, but also Thread 1 could attempt to raise f1 when f1 is already up, leading to the ERRor state. In fact, this barrier works correctly once, but it is not reusable: in the erroneous path, Thread 1 races to the second iteration of the loop and attempts to raise f1, while Thread 2 has not yet completed its lower operation in the first iteration. This is the kind of subtle interleaving-dependent issue that makes concurrent programming hard (and fun).

Now let’s see how we can automate this analysis. I will use CIVL, but any standard model checker will do. Here is a CIVL-C model of the first (correct) barrier program:

A flag is just a Boolean variable. The restriction on raise is checked by an assertion. The “when” statement in function lower causes the caller to block until the condition in parentheses is true, then executes the body of the statement; the check that the condition is true and execution of *f = 0 occur atomically, i.e., no other thread executes between those two points.

Running CIVL on this program yields:

The key part of the output is “The standard properties hold for all executions”, indicating the assertion is never violated. Let’s do the same for the erroneous protocol:

Checking…

The output indicates the assertion is violated and shows that process 1 (i.e., Thread 1) is in the “raise” call while process 2 is just before the lower. We can see more details, including a blow-by-blow account of the execution that arrived at that point, as follows:

That, in a nutshell, is how you can use a model checker to verify, or find a bug in, a concurrent algorithm. And if you are a teacher looking for examples of simple “truthy” concurrent protocols with subtle bugs, you can’t do much better than this erroneous 2-thread barrier.